
When you’re hauling a couch through a narrow hallway and yelling “Pivot!” like Ross from Friends, you’re unwittingly grappling with a half-century-old mathematical conundrum. Known as the Moving Sofa Problem, this brain teaser asks a deceptively simple question: What’s the largest sofa you can fit around a 90-degree corner without getting stuck?
For over 50 years, mathematicians have wrestled with this problem, proposing increasingly intricate shapes in search of an answer. Now, Jineon Baek, a postdoctoral researcher at Yonsei University in South Korea, believes he has finally solved it.
Baek’s 100-page proof, posted on the arXiv preprint server in early December, concludes that the largest sofa capable of squeezing around the corner has an area of 2.2195 units.
The Gerver Sofa: A Shape with 18 Curves

The Moving Sofa Problem was first posed by Austrian-Canadian mathematician Leo Moser, who wanted to know the optimal shape for moving a large object through a hallway corner. Over the decades, various mathematicians chipped away at the problem, but a definitive proof remained elusive.
In 1992, Joseph Gerver, a mathematician from Rutgers University, proposed the Gerver sofa, an elaborate U-shaped figure composed of 18 curves. Imagine assembling this beast if it came from IKEA. This design suggested the largest possible sofa could have an area of 2.2195 units. Though no one could prove that Gerver’s shape was the optimal solution, no one found a better one either.
Baek’s breakthrough refines Gerver’s work. By applying modern mathematical tools and carefully analyzing the geometry, Baek demonstrated that Gerver’s sofa is indeed the largest that can make the turn. His calculations confirm that no shape larger than 2.2195 units can navigate the corner. One unit represents the width of the hallway.

Why is This Important?

While the Moving Sofa Problem sounds like an abstract exercise — or a practical joke on frustrated movers — it represents a broader challenge in geometry and optimization. It forces mathematicians to explore the limits of shape and space, often revealing new mathematical insights.
The problem also shows how real-world frustrations can evolve into serious academic pursuits. Whether it’s fitting furniture or optimizing routes for autonomous robots, understanding how objects move through constrained spaces has wide-ranging applications.
Interestingly, there’s even a variant of the problem called the Ambidextrous Sofa Problem. This involves navigating two corners, one turning left and the other turning right. The best-known solution to this challenge, proposed by mathematician Dan Romik, is as rigorous as it is entertaining.
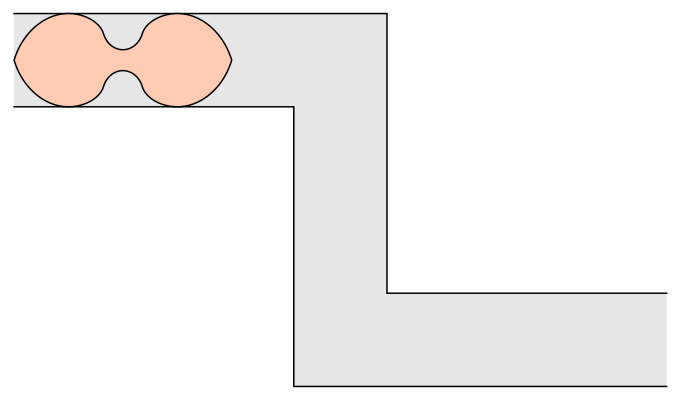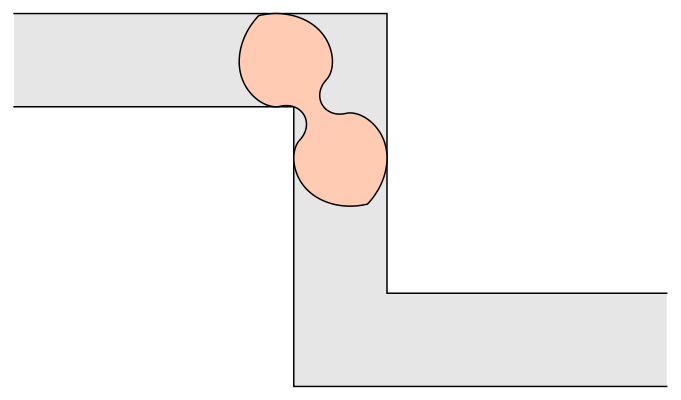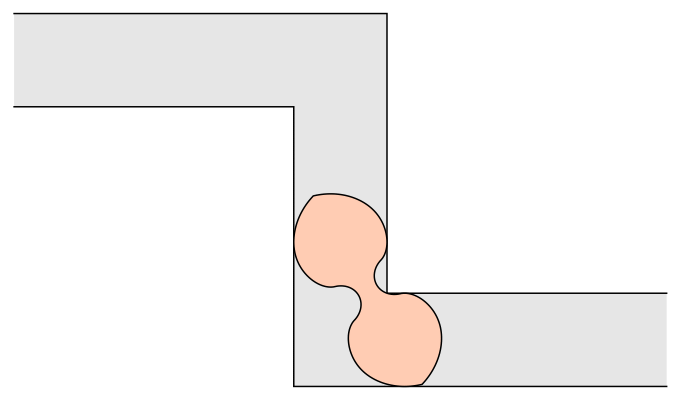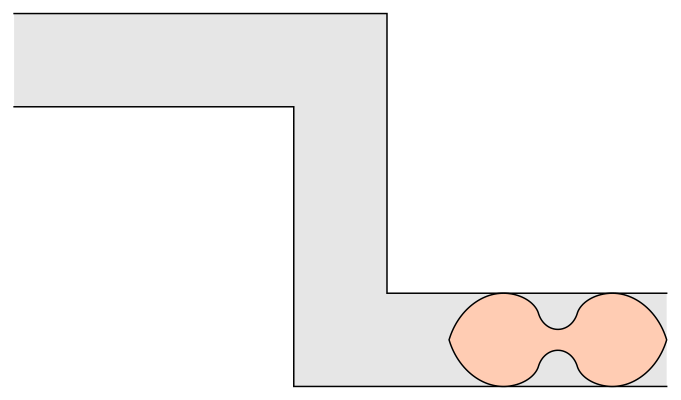
“It’s a surprisingly tough problem,” said Romik, who is a math professor and chair of the Department of Mathematics at University of California Davis. “It’s so simple you can explain it to a child in five minutes, but no one has found a proof yet.
You can learn more about it in this fantastic Numberphile video.
The Road to Verification
Baek’s work is not yet peer-reviewed, a crucial step in mathematical research. As with any major proof, other mathematicians will scrutinize his work to verify its accuracy. But the initial reception has been one of cautious excitement.
Images of the Gerver sofa spread across social media following Baek’s announcement, with mathematicians and enthusiasts alike marveling at the possibility that this long-standing puzzle may finally be solved. If Baek’s proof holds, it will close a chapter that began in the 1960s, offering a neat solution to a problem that seemed endlessly unsolvable.
Until then, if you’re moving furniture, maybe just pick a building with straight hallways.


