Our eyes and brain are designed to interpret the world around us from a three-dimensional perspective. Understanding a higher-dimensional world is a stretch of the imagination for most people and no one can actually visualize more than three dimensions — just like a 2-D ‘flat-lander’ has no hope of visualizing 3-D. Neuroscientists, however, claim that our brain, which never ceases to amaze us it seems, is comprised of structures that are seven dimensions, some up to eleven dimensions.
“We found a world that we had never imagined,” says neuroscientist Henry Markram, director of Blue Brain Project and professor at the EPFL in Lausanne, Switzerland, “there are tens of millions of these objects even in a small speck of the brain, up through seven dimensions. In some networks, we even found structures with up to eleven dimensions.”
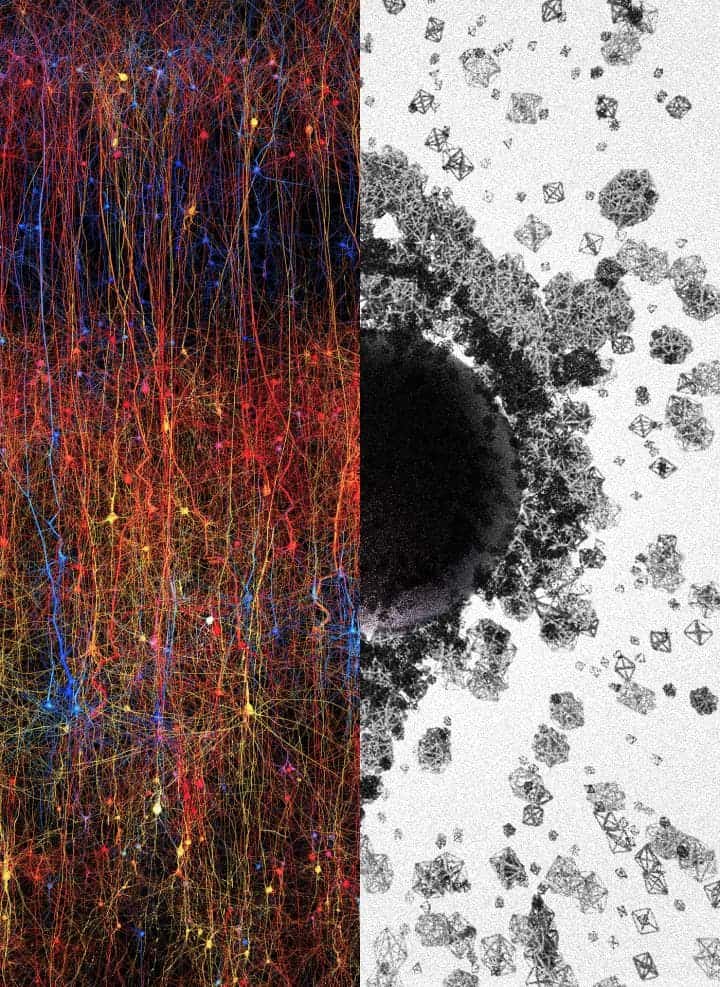
The human brain is the least understood of any human body part — not coincidentally, it’s also the most complex. According to Makram and colleagues working with the Blue Brain Project — an initiative that aims to create a digital reconstruction of the brain by reverse-engineering mammalian brain circuitry — these mind-boggling higher-dimensional structures can partly explain why it’s so hard to understand the brain. But what does that mean, really?
“The progression of activity through the brain resembles a multi-dimensional sandcastle that materializes out of the sand and then disintegrates”
Kathryn Hess from EPFL and Ran Levi from Aberdeen University are skilled in an obscure but edifying branch of mathematics called algebraic topology, the study of the global properties of spaces by means of algebra. To get an idea of what algebraic topology is about, think about the fact that we live on the surface of a sphere but locally this is difficult to distinguish from living on a flat plane. Algebraic topology is concerned with the whole surface and points to the obvious fact that the surface of a sphere is a finite area with no boundary and the flat plane does not have this property.
What makes algebraic topology so powerful has always been its wide degree of applicability to other fields from physics, to number theory, to differential geometry. This is the firs time it has been used in neuroscience, though.
“Algebraic topology is like a telescope and microscope at the same time. It can zoom into networks to find hidden structures – the trees in the forest – and see the empty spaces – the clearings – all at the same time,” explains Hess.
Two years ago, the Blue Brain released the first digital copy of a partial neocortex. The neocortex is the portion of the human brain that is responsible for language and consciousness. It’s the most evolved part of the brain and makes up approximately 76% of the human brain, making it the largest when compared to similar structures in other animals. Now, with the help of algebraic topology, Blue Brain researchers showed that the multi-dimensional brain structures discovered could never be produced by chance, based on studies of the virtual brain. Later, experiments on real brain tissue confirmed the virtual findings suggesting that the brain constantly rewires during development to build a network with as many high-dimensional structures as possible.
Were it not for algebraic topology, the researchers couldn’t have been able to discern highly organized structures hidden in the seemingly chaotic firing patterns of neurons.
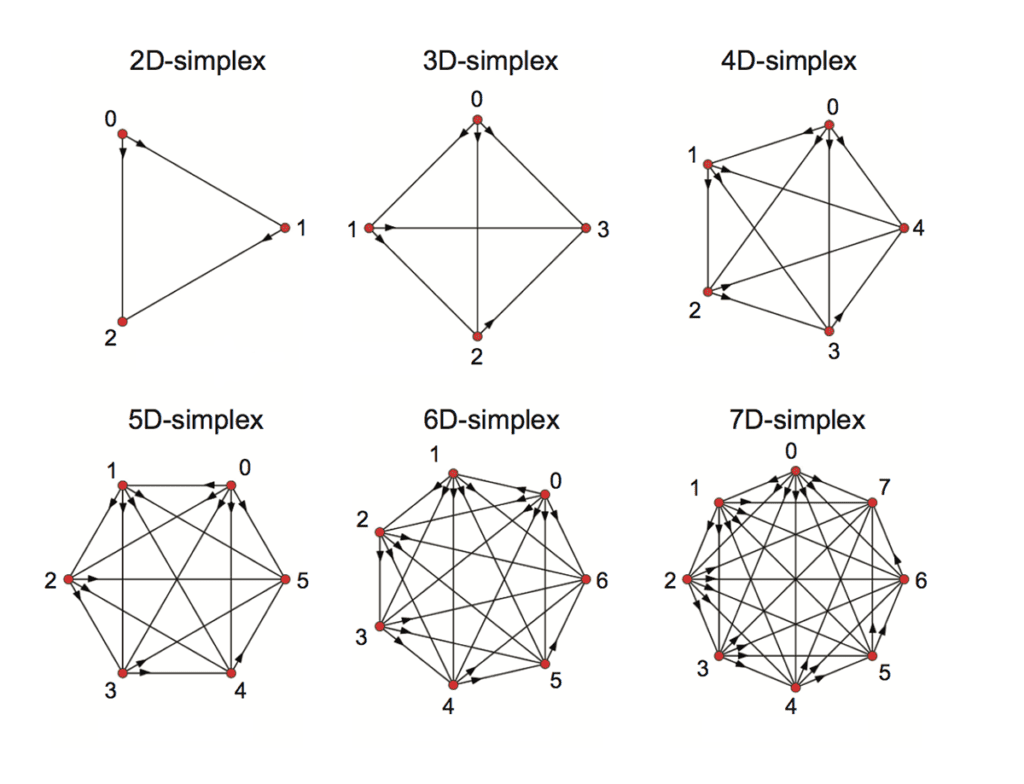
When a stimulus was made onto the virtual brain tissue, cliques of progressively higher dimensions assembled momentarily to enclose high-dimensional holes or cavities as the researchers refer to them. The more neurons there are in a clique, the higher the ‘dimension’ of the object. Some speculate it’s in these cavities that memories may be stored in the brain.
“The appearance of high-dimensional cavities when the brain is processing information means that the neurons in the network react to stimuli in an extremely organized manner,” says Levi. “It is as if the brain reacts to a stimulus by building then razing a tower of multi-dimensional blocks, starting with rods (1D), then planks (2D), then cubes (3D), and then more complex geometries with 4D, 5D, etc. The progression of activity through the brain resembles a multi-dimensional sandcastle that materializes out of the sand and then disintegrates.”
The team is now trying to understand whether there’s any relation between these multi-dimensional ‘sandcastles’ and cognition.
Findings appeared in the journal Frontiers in Computational Neuroscience.


