At the beginning of the 20th Century, physicists were developing the field of quantum physics, discovering in the process that the rules they had grown comfortable with no longer applied at the smallest scales. For example; the argument about the nature of light — was it particle or wave — that had raged for decades could be answered only by concluding it is neither but has properties of both. Furthermore, they found that this particle/wave duality applies to matter particles like electrons too.
German theoretical physicist Werner Heisenberg was about to make his own shocking discovery, he was about to find that nature imposes a fundamental limit on what even the most aspiring physicists could know.
He would formulate this concept into the uncertainty principle.

In 1925, Heisenberg would publish a paper that informed physicists that nature has a way of telling you that you can’t have your cake and eat it too. Something intrinsic and built into the fabric of the very Universe that reminds you that no matter how smart you are, no matter how sophisticated your experimental method, and how sensitive your equipment, you can’t ‘know’ everything about a system. An idea that contradicts the principles that classical physics was built upon.
Assuming the name Heisenberg’s uncertainty principle, the Heisenberg uncertainty principle, or simply, the uncertainty principle, the concept would become arguably the second most commonly recognised element of quantum physics, outside of Schrodinger’s eponymous feline. Eventually, this idea would find itself absorbed into pop culture, making its way to jokes, newspaper strips, t-shirts, and cartoons.
“The uncertainty principle ‘protects’ quantum mechanics,” said legendary physicist Richard Feynman of the utility of Heisenberg’s breakthrough. “Heisenberg recognized that if it were possible to measure both the momentum and the position simultaneously with greater accuracy, quantum mechanics would collapse. So he proposed that must be impossible.”
What is the Uncertainty Principle?
The most generalised version of Heisenberg’s uncertainty principle says that if you measure the momentum of a particle with uncertainty Δp, then you are limited in how precisely you can ‘know’ its position. You can’t know it any more precisely than Δx ≥ ℏ/2Δp, where ℏ (or H-bar) is a value known as the reduced Planck’s constant and is extremely small, a fact that will become important when we ask why macroscopic objects like cars and balls don’t seem to be affected by the uncertainty principle.
Rearranging the equation above gives the most common version of Heisenberg’s uncertainty principle, and perhaps the most famous equation in physics outside of E=mc^2. This equation tells us that when the uncertainty in position is multiplied by the uncertainty in momentum its value can’t be greater than the reduced Planck’s constant divided by two.
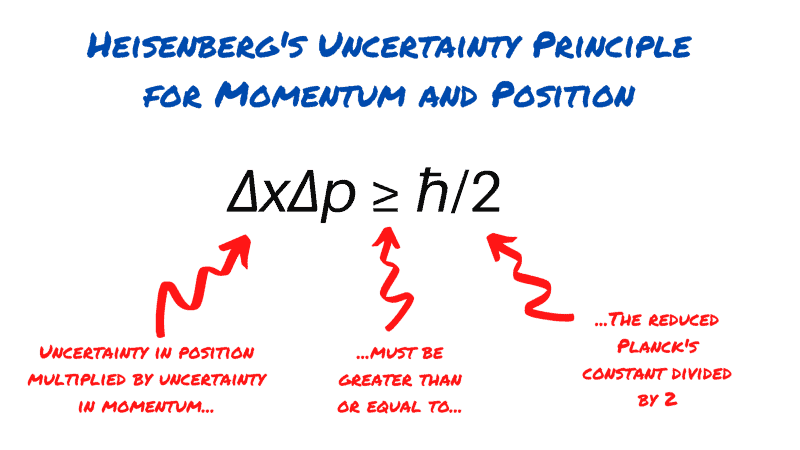
The equation above also applies to several other variables, most notably energy and time, it can also be adapted to any suitable pairs of operators in a system.
The momentum and position version of the uncertainty principle may well be the most familiar but it is by no means the only version, nor should the other versions be considered less important. In fact, the energy/time variation of the uncertainty principle gives rise to one of the most striking and counter-intuitive elements of reality — the idea that virtual pairs of particles can pop in and out of existence.
If you consider an infinitesimal isolated area of spacetime observed for a precisely ‘known’ period of time, then the uncertainty principle for energy and time (ΔE Δt = ≥ ℏ/2Δ) says that you can’t precisely know the energy content of that area. Meaning that particles must be popping in and out of existence in that box.

This concept, wittily named ‘nature’s overdraft facility’ by some waggish physicists, is a phenomenon that sounds unlikely, impossible even, but has been experimentally verified. The Heisenberg uncertainty principle limits just how long the Universe will allow itself to go ‘overdrawn’ before the particles annihilate and that energy loan is paid back.
In order to get aspiring physicists to accept the radical ideas birthed from the uncertainty principle, and the concept that there is a fundamental limit to what can be known about a system — something contrary to classical physics —thus meaning that everything classical physics imparts about the ‘knowability’ of a system is wrong, a ‘semi-classical’ version was first presented to the scientific community.
We approach it now with some trepidation and the warning that it barely scratches the surface of the uncertainty principle and somewhat downplays how intrinsic it is in nature.
The Semi-Classical Uncertainty Principle
You’re asked to take part in a quantum physics experiment at the ZME labs. You arrive, are immediately handed a tennis racquet and asked to step into an extremely dark room. Once in there, a voice announces that your task is simply to find the tennis balls in the room with the racquet.
“Sounds simple enough,” you think. That is until a tennis ball strikes your leg at high-speed. You realise that the tennis balls are being fired into the room at completely random angles. Eventually, after some failing around in the dark, you’re racquet hits a ball. “Got one!” you exclaim.
“That’s great,” comes the voice over the intercom. “Where is it now?”
Of course, the problem with that crude little analogy is that the very act of ‘measuring’ the ball’s position or momentum, intrinsically changes the state of the system and essentially puts you back at square one. It’s a little like that every time we try to take a quantum mechanical measurement.
In order to ‘see’ an electron, researchers have to fire photons at it. The problem is that photons carry with their momentum. And as electrons are so small, the wavelengths of the photons have to be of a similar scale. The issue is, the shorter the wavelength, the higher the energy and, in turn, the greater the momentum.
Thus, bombarding an electron with photons imparts this moment to them, changing the very state of the system.
The reason that the semiclassic description of the Heisenberg uncertainty principle is that it gives the impression that if there was some incredibly sensitive measuring technique, it could, perhaps, be ‘worked around.’ This isn’t true. No matter how sensitive, this relationship is something that can’t really be avoided. It’s ‘built-in’ to nature.
To see why this is the case it’s necessary to investigate one of the founding principles of quantum mechanics, the ubiquitousness of waves.
Wave Certainty Goodbye
You receive a call from ZME labs. “We know the last experiment didn’t go so well, and we really hope the bruises are healing,” says a painfully familiar voice. “Look, we’ve got another test and this one will really demonstrate Heisenberg’s uncertainty principle… no tennis balls.”
You reluctantly agree to attend.
Upon your arrival, you are handed a skipping rope and asked to wave it up and down rhythmically. The opposite end is held by a nervous-looking lab assistant who you notice is covered in tennis ball-sized welts.
Below is what results from your frantic, yet rhythmically waving. A steady wave shape. But, here comes the voice through the loudspeaker again: “Ok, now tell us, where on the x-axis [which marks position] is the wave?”
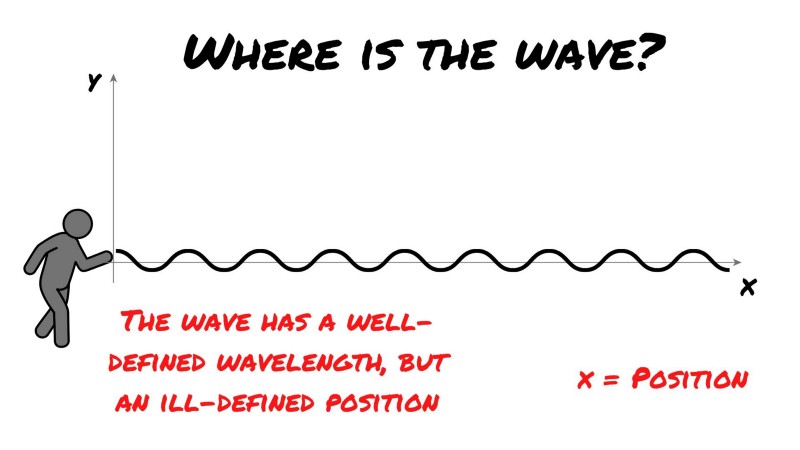
As you can see, the wave has no well-defined position, and here is how that is analogous to a particle in quantum mechanics. In the mathematics used to describe a quantum system, the spread of the wave is momentum, and the square of the amplitude is the probability of the particle being located in a particular position.
Thus, in the above image what we actually have is a very well-known momentum. And as Heisenberg’s uncertainty principle primes us to believe, we can see that we can say nothing about the position as the wave can’t be said to possess a single position on the x-axis. The square of the amplitude is the same everywhere.
Back to ZME labs. You’ve had just about enough of these cryptic unanswerable questions and bizarre sports-equipment-related experiments. So to teach the researchers a lesson, you give the rope one sudden ‘whip’ — Indiana Jones style.
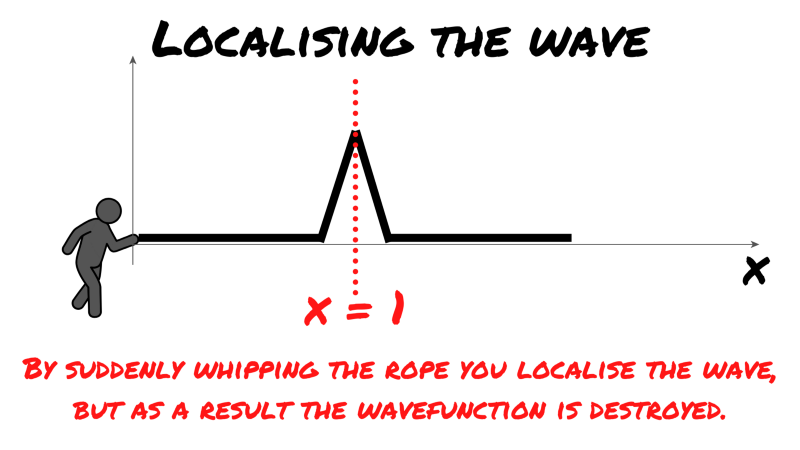
The wave is suddenly localised, as you can see, the amplitude and thus the square of the amplitude is zero everywhere but in one spot. A position can be assigned to the wave, but as you can see, there is no spread anymore — the wave function is destroyed.
This is analogous to having exact knowledge of a particle’s location. As the wavefunction spread is destroyed and this was the representation of the particle’s momentum, you suddenly have no knowledge of momentum.
All this shows that Heisenberg’s uncertainty principle really arises from the fact that matter can be described as waves on the quantum level.
You are on your way out of ZME labs, for what you hope is the final time and nursing serious whiplash in your wrist when the lead researcher hands you a tennis ball. “As a memento,” he says chirpily.
You thank him, but mentally vow to throw it over the tallest wall you can find on the way to your car and home.
Little do you know, your rage against the ball will reveal how without the phenomena described by Heisenberg’s uncertainty principle the Universe would be a much colder, and darker place.
Quantum tunnelling: Quantum balls and tall walls
One of the most remarkable features of the quantum realm is the phenomenon of quantum tunnelling, without which the nuclear fusion processes that power the stars and create the Universe’s heavier elements would not be able to take place.
Tunnelling allows protons in the core of the sun to overcome mutual repulsion caused by their positive charges, a potential barrier that even under extreme pressure, they do not have the kinetic energy to overcome. This allows the formation of deuterium from hydrogen nuclei and begins the nuclear fusion process in the star’s core which leads to the formation of helium from hydrogen and powers its immense energy output.
You’re thinking about quantum tunnelling on your way to your car when you feel the tennis ball you received as a ‘memento’ and stuffed in your pocket pressing into your thigh. Remembering your promise, you look at the nearest wall, noting that it’s probably higher than you can throw the ball.
You resolve to give it a few tries anyway.
You throw the ball a few times, each with exactly the same force against the same resistance provided by gravity and air resistance, realising you can’t give it enough kinetic energy to get it over the top of the wall. In fact, you’re falling considerably short. But, this is a special ball. The researchers at ZME labs have found a way to imbue it with the qualities of a quantum particle.
On your 47th throw of the quantum ball with the same kinetic energy, the ball approaches its usual limit and simply disappears. You inspect the wall seeing no holes, and you know there is no way the ball could have broken through the wall… then you hear a loud cry from over the side of the wall scream: “My flowers… Whose ball is this?” You decide discretion is the better part of valour, and flee the scene.

So, how can Heisenberg’s uncertainty principle be responsible for the ball travelling to the other side of the wall, an area that in physics we would describe as ‘classically forbidden’?
The key is, that as we precisely know this quantum ball’s momentum, we can’t be sure of its position. This means that there is a tiny probability that the ball can be found in a region it should be impossible to reach.
Below, you can see a simulation of what happens when a particle of certain energy approaches an energy barrier that exceeds its energy. It should be noted here that the ‘wider’ or ‘taller’ the barrier, ie. the greater the energy demand, the less likely a particle is to clear it.
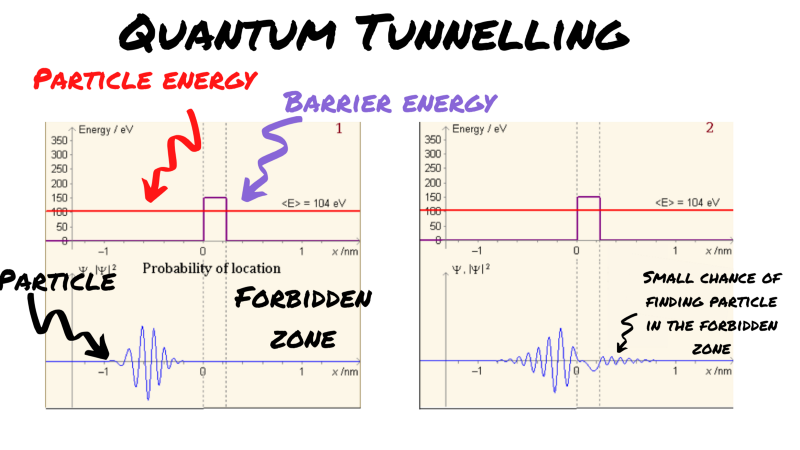
You can think about tunnelling like this. A particle of energy <E> approaches a barrier of <2E>. Clearly, it doesn’t have enough energy to ‘jump’ this barrier. Yet, in quantum physics, we find a small probability that transmission occurs. Obviously, that means that in circumstances where you have a lot of particles, like in the core of a star, the law of large numbers suggests that this kind of rare event still happens a lot.
As you muse on this, you have a worrying thought: “I know the exact momentum of my car. Does that mean I can’t know its position?”
You quicken your step considerably.
Dude where’s my car? Why Heisenberg’s uncertainty principle doesn’t apply to everyday objects
Heisenberg and Schrödinger get pulled over for speeding. The cop asks Heisenberg: “Do you know how fast you were going?”
Heisenberg replies: “No, but we know exactly where we are!”
The officer looks at him confused and says: “you were going 108 miles per hour!”
Heisenberg throws his arms up and cries: “Great! Now we’re lost!”
We’ve thus far had a little fun describing macroscopic objects like tennis balls and skipping ropes displaying quantum behaviour, so it’s probably an idea to explain why this isn’t something we actually see every day.
The key is the very small value of the reduced Planck’s constant (ℏ). This means that the lower limit in the uncertainty of measuring the position and momentum of large objects is negligible when compared to massive objects like tennis balls, skipping ropes or cars.
All matter has a de Broglie wave (λdb) but that wave has to be a comparable size to Planck’s reduced constant for Heisenberg’s uncertainty principle to have a considerable effect. The de Broglie wave of a tennis ball is way too small to be subject to the uncertainty principle in any significant way.
It’s for much the same reason that moving objects don’t diffract around trees. Their de Broglie wave is way too small.
Sorry, you’re not getting off with that speeding ticket so easily.
Sources and further reading
Griffiths. D. J, ‘Introduction to Quantum Mechanics,’ Cambridge University Press, [2017].
Feynman. R, Leighton. R. B, Sands. M, ‘The Feynman Lectures on Physics. Volume III: Quantum Mechanics,’ California Institute of Technology, [1965].
Bolton. J, Lambourne. R, ‘Wave Mechanics,’ The Open University, [2007].


